কোয়ান্টাম বিজ্ঞান ও প্রযুক্তির আন্তর্জাতিক বর্ষে স্কুলের ছাত্র-ছাত্রীদের জন্য দেওয়া একটা বক্তৃতা

কলমে: অম্লান রায়

Variable Energy Cyclotron Centre, Kolkata, India

---

অনেকেই জানেন যে ২০২৫ সালটাকে জাতিসঙ্ঘের শিক্ষা , বিজ্ঞান ও সাংস্কৃতিক সংস্থা (UNESCO) কোয়ান্টাম বিজ্ঞান ও প্রযুক্তির আন্তর্জাতিক বর্ষ হিসাবে ঘোষণা করেছেন। কারণ এই বছর সগৌরবে কোয়ান্টাম বিজ্ঞানের শতবর্ষ পূর্ণ  হল। এই উপলক্ষে American Physical Society (APS) আমেরিকার বিভিন্ন হাইস্কুলে (ক্লাস ১১ -১২) কোয়ান্টাম বিজ্ঞান ও প্রযুক্তি নিয়ে বক্তৃতার আয়োজন করেছে। উদ্দেশ্য হচ্ছে স্কুলের ছাত্র-ছাত্রীদের কোয়ান্টাম বিজ্ঞান ও প্রযুক্তিতে আগ্রহী করে তোলা। এই রকম একটা বক্তৃতা আমিও দিয়েছিলাম ZOOM Link এর মাধ্যমে। আমি বক্তৃতা দিয়েছিলাম Hampton, Virginia, USA  এর একটা হাই-স্কুলের ছাত্র-ছাত্রীদের কাছে। স্কুলটার নাম New Horizon Regional Education Centers, Governor’s School for Science and Technology। আমাকে বলা হয়েছিল যে আমার নিজের পরিচয় দিয়ে আমি নিজে হাই-স্কুলে পড়ার সময় প্রথম কি ভাবে কোয়ান্টাম বিজ্ঞানের সাথে পরিচিত হয়েছিলাম, সেই পরিপ্রেক্ষিতে বক্তৃতা শুরু করতে এবং অবশ্যই যেন হাই-স্কুলের (ক্লাস ১১-১২) ছাত্রদের বোধগম্য হয়। নির্দিষ্ট দিনে ৩০ জন ছাত্র-ছাত্রী ও তাদের শিক্ষিকা ZOOM Link এর মাধ্যমে আমার বক্তৃতা শোনার জন্য উপস্থিত হয়েছিলেন এবং প্রায় ঘণ্টা দেড়েক ধরে আমার কথা শোনেন। অন্য ছাত্র-ছাত্রীদের আমার বক্তৃতার Video Recording শোনাবেনও বলেন। তবে ছাত্র-ছাত্রীদের মধ্যে কোয়ান্টাম বিজ্ঞান নিয়ে কতটা উৎসাহ ও আগ্রহ সৃষ্টি করতে পেরেছিলাম, তা বলতে পারবো না। তবে যা বলেছিলাম, সংক্ষেপে এখানে লিখছি।

বক্তৃতা

সকলকে Good Morning, আমার এখানে এখন Good Evening। ভারতবর্ষের পূর্বপ্রান্তে কলকাতা থেকে বলছি।

কোয়ান্টাম বিজ্ঞানের সাথে তোমাদের কিছুটা পরিচয় করানোর উদ্দেশ্য নিয়ে এই বক্তৃতা। প্রথম কথা হল কেন কোয়ান্টাম বিজ্ঞান পড়বো? আজকের দিনে তোমাদের চারিদিকে কোয়ান্টাম বিজ্ঞানের ব্যবহার দেখছ। সৌর প্যানেল যা দিয়ে সূর্যের আলোকে বিদ্যুতে পরিণত করা হয়, semiconductor যা দিয়ে তোমাদের cell phone, computer চলছে , চিকিৎসার জন্য MRI, Nuclear medicine, নানারকম বিস্তারিত বিশ্লেষণের জন্য Electron microscope ইত্যদি অনেক কিছুই কোয়ান্টাম বিজ্ঞানের ব্যবহার। এছাড়াও জীববিজ্ঞানে DNA কে মডেল করার জন্য কোয়ান্টাম গণনা করা হচ্ছে। তাছাড়া আসছে কোয়ান্টামের সাহায্যে গুপ্ত লিপি প্রেরণ এবং কোয়ান্টাম কম্পিউটার। কাজেই আগামী প্রজন্মকে কোয়ান্টামে পারদর্শী হতেই হবে।

এইবার আসি আমি কি ভাবে কোয়ান্টাম বিজ্ঞানে আগ্রহী হয়েছিলাম, সেই কথায়। আমার কৈশোরে অবশ্য কোয়ান্টামের এই রকম ব্যাপক ব্যবহার ছিল না। স্কুলের রসায়ন বিজ্ঞানের ক্লাস থেকেই কোয়ান্টাম বিজ্ঞানে প্রথম আগ্রহ হয়েছিল। কলকাতার কাছেই হুগলী জেলায় চুঁচুড়া শহরে গঙ্গা নদীর তীরে অবস্থিত হুগলী কলেজিয়েট স্কুল থেকে আমি উচ্চমাধ্যমিক পাস করেছিলাম। স্কুলে পদার্থবিজ্ঞান ও রসায়ন বিজ্ঞান পড়েছিলাম। রসায়ন বিজ্ঞানের ক্লাসেই প্রথম অণু ও পরমাণুর কথা শুনি এবং সেখান থেকেই কোয়ান্টাম বিজ্ঞান নিয়ে আগ্রহ জন্মায়।

স্কুলের রসায়ন বিজ্ঞানের ক্লাসে আসা যাক। তোমরাও সবাই নিশ্চয় গ্যাসের সূত্র অর্থাৎ Boyle’s law, Charles’s law পড়েছ। নির্দিষ্ট পরিমাণ গ্যাসের তাপমাত্রা স্থির রেখে চাপ বাড়ালে তার আয়তন আনুপাতিক ভাবে কমে (Boyle’s law) এবং চাপ স্থির রেখে তাপমাত্রা বাড়ালে আয়তন আনুপাতিক ভাবে বাড়ে (Charles’s law)। এর থেকেই আসে যে নির্দিষ্ট পরিমাণ গ্যাসের ক্ষেত্রে চাপ ও আয়তনের গুণফল সমান হয় কত পরিমাণ গ্যাস আছে (মোলের হিসাবে ), সর্বজনীন গ্যাস ধ্রুবক ও তাপমাত্রার গুণফলের সাথে। নির্দিষ্ট পরিমাণ গ্যাসকে কি ভাবে মোলের হিসাবে লিখতে হয়, তা আমাদের রসায়নের শিক্ষক শম্ভুবাবু শিখিয়েছিলেন এবং এখান থেকেই অণু-পরমাণুর ধারণা আসে। এক মোল যে কোন পদার্থে একটা নির্দিষ্ট সংখ্যক অণু বা পরমাণু থাকে। আপাতত পরমাণু নিয়েই আলোচনা করছি। একটা মৌলের পরমাণু হচ্ছে তার ক্ষুদ্রতম কণিকা, যার মধ্যে ওই মৌলের সব রাসায়নিক ধর্ম  থাকে। এক মোল লোহা , সোনা , রূপা, তামা সবেতেই একটা নির্দিষ্ট সংখ্যক পরমাণু থাকে। এক মোল লোহা মানে প্রায় ৫৬ গ্রাম লোহা, সোনা অনেক বেশি ভারি বলে এক মোল সোনার ভর প্রায় ১৯৭ গ্রাম। অর্থাৎ এক মোল মানে ভরের দিক দিয়ে খুব বেশি কিছু নয়, বেশিরভাগ ক্ষেত্রেই বিশ-পঞ্চাশ-একশো গ্রামের মত পদার্থ। কিন্তু এই সামান্য পরিমাণ পদার্থে অর্থাৎ এক মোল পদার্থে কত সংখ্যক পরমাণু থাকে , তা শুনলে মাথা ঘুরে যাবে। তোমরাও  জানো এই বিশাল সংখ্যাটাকে অ্যাভোগাড্রোর সংখ্যা বলা হয় এবং এটা হচ্ছে প্রায় ছয় শত কোটি কোটি কোটি (৬×১০^২৩ )। কি করে এই বিশাল সংখ্যাটা পাওয়া গেল? গ্যাসের সূত্র অর্থাৎ Boyle’s law, Charles’s law যদি একেবারে সঠিক হত, তাহলে একটা পরমাণুর আয়তন শূন্য হত, অর্থাৎ এক মোল গ্যাসে অসীম সংখ্যক পরমাণু থাকতে পারত এবং অ্যাভোগাড্রোর সংখ্যা অসীম হত। কিন্তু আরও সূক্ষ্ম পরীক্ষায় দেখা গেল Boyle’s law, Charles’s law একেবারে সঠিক নয়, বিশেষত উচ্চ চাপের গ্যাসের ক্ষেত্রে। এই সংশোধিত গ্যাসের সূত্র থেকেই জানা গেল যে খুব ছোট হলেও পরমাণুর একটা আয়তন আছে এবং অ্যাভোগাড্রোর সংখ্যা অনেক বড় হলেও অসীম হবে না। সংশোধিত গ্যাসের সূত্র এবং গ্যাসের সান্দ্রতার (viscosity) পরিমাপ থেকে প্রথম জানা গেল যে একটা পরমাণুর ব্যাসার্ধ ১০^-৮ সেন্টিমিটার। অর্থাৎ পরমাণুর ব্যাসার্ধ আমাদের মাথার একটা চুল যত সরু, তার থেকেও প্রায় লক্ষ গুণ কম। পরমাণুর আয়তন এতো ছোট বলেই অ্যাভোগাড্রোর সংখ্যাটি এতো বিশাল (৬×১০^২৩)।

মাথার একটা চুল যত সরু, তার চেয়েও লক্ষ গুণ কম ব্যাসার্ধের পরমাণুর কথা না হয় গণনা করে জানলাম, চোখে দেখা কি যাবে? দুর্ভাগ্যবশত কোন magnifying glass দিয়েই চোখে দেখা যাবে না। কারণ আমাদের চোখ কেবলমাত্র দৃশ্যমান আলোয়  (লাল, সবুজ, নীল , বেগুনী) দেখতে পায় এবং এই আলোর তরঙ্গদৈর্ঘ্য  মাথার চুলের ব্যাসার্ধ এর চেয়ে মাত্র কয়েক শত গুণ কম। কাজেই ওত বড় তরঙ্গদৈর্ঘ্য ব্যবহার করে মাথার চুলের চেয়ে লক্ষ গুণ ছোট পরমাণুকে দেখা যাবে না। এক্স রে দিয়েও হবে না। গামা রশ্মি দিয়ে তাত্ত্বিক ভাবে সম্ভব হলেও, তা দিয়ে ক্যামেরা বানানো সম্ভব নয়। কারণ গামা রশ্মি বস্তুকে ভেদ করে চলে যায়, তাকে ফোকাস করা যায় না এবং উচ্চ শক্তির গামা রশ্মি বস্তুর মধ্যে তার চরিত্র বদলে ফেলে।

কোন কণা যেমন ঋণাত্মক তড়িৎযুক্ত ইলেকট্রন কণা ব্যবহার করে কি পরমাণুর ছবি তোলা যেতে পারে? কণার কথা বললে ধূলি কণার কথা মনে আসে। কিন্তু তার চরিত্র তো স্থানীয়ভাবে এক জায়গায় থাকা। অবশ্যই গতিশীল কণা সরলরেখায় যায় এবং তড়িৎযুক্ত কণার স্রোতকে, যেমন ইলেকট্রন কণার স্রোতকে ফোকাস করা যায়। কণার স্রোত কোন বস্তুর উপর পড়ে তার পিছনে ছায়া প্রতিবিম্বের সৃষ্টি করে। কিন্তু এই ছায়া প্রতিবিম্বের সাহায্যে উচ্চ মানের বা উচ্চ বিশ্লেষণ ক্ষমতাসম্পন্ন ছবি তোলা যায় না। উচ্চ বিশ্লেষণ ক্ষমতার ছবি তোলার জন্য তরঙ্গ এর ব্যবহার আবশ্যিক। তরঙ্গের ব্যতিচার ও বিবর্তন ধর্মের জন্যই ছায়া প্রতিবিম্বকে অতিক্রম করে উচ্চ মানের ছবি তোলা যায়। বস্তুর আকারের সূক্ষ্ম পার্থক্যগুলি তরঙ্গের বিস্তার ও দশার পরিবর্তন ঘটায় এবং তরঙ্গকে ফোকাস করলে এই সূক্ষ্ম পার্থক্যগুলি প্রাবল্যের পরিবর্তন ঘটিয়ে ক্যামেরায় ধরা পড়ে। যত ছোট তরঙ্গদৈর্ঘ্য ব্যবহার করা হবে, ততই বেশি  বিশ্লেষণ ক্ষমতার ছবি তোলা সম্ভব হয়। কাজেই ইলেকট্রন বা কোন কণার সাহায্যে পরমাণুর ছবি তুলতে গেলে, তার একাধারে অবশ্যই তরঙ্গ ধর্ম থাকতে হবে, শুধু কণা ধর্ম থাকলে ছায়া প্রতিবিম্বের বেশি কিছু হবে না, আবার অন্যদিকে তার তরঙ্গদৈর্ঘ্য পরমাণুর ব্যাসার্ধের চেয়েও অনেক ছোট হতে হবে।

কিন্তু এতো আপাত দৃষ্টিতে পরস্পর-বিরোধী প্রস্তাব দেওয়া হচ্ছে। বলছি কণার সাহায্যে ছবি তুলবো, আবার তার তরঙ্গধর্ম না থাকলেও উচ্চমানের ছবি তোলা যাবে না এবং তার তরঙ্গদৈর্ঘ্যকে খুব ছোট হতে হবে। ইলেকট্রনের কি তরঙ্গধর্ম থাকতে পারে? ১৯২৭ সালে আমেরিকার বেল ল্যাবরেটরিতে Davisson ও Germer ইলেকট্রনের স্রোতকে নিকেলের কেলাসের উপর ফেলে ইলেকট্রনের বিবর্তন ফ্রিঞ্জ দেখেন, অর্থাৎ ইলেকট্রনের তরঙ্গ ধর্মের প্রমাণ পাওয়া গেল। গ্যাসের উপর ইলেকট্রনের স্রোত ফেলেও বিবর্তন ফ্রিঞ্জ দেখা গেল (১ নং ছবি)।     

১ নং ছবি :  ৬০ keV ইলেকট্রনের স্রোতকে বেঞ্জিন গ্যাসের উপর ফেলে পাওয়া বিবর্তন ফ্রিঞ্জ।

কিন্তু ইলেকট্রনের তরঙ্গদৈর্ঘ্য কত হয়? জানা গেল যে ইলেকট্রনের তরঙ্গদৈর্ঘ্য তার ভরবেগের ব্যস্তানুপাতিক হয়। ২০০ keV ইলেকট্রনের তরঙ্গদৈর্ঘ্য পরমাণুর ব্যাসার্ধের চেয়েও একশো গুণ কম। এই ২০০ keV ইলেকট্রনের স্রোত  ব্যবহার করেই পরমাণুর উচ্চ মানের ছবি তোলা সম্ভব হল (২ নং ছবি)। শুধু তাই নয় আরও অনেক উচ্চ বিশ্লেষণমূলক কাজ Electron Microscope এর সাহায্যে বর্তমানে করা হয়।

২  নং ছবি :  ২০০ keV ইলেকট্রনের স্রোতের সাহায্যে উচ্চ বিশ্লেষণ ক্ষমতায় তোলা মলিবডেনাম সালফাইডের কেলাসের পরমাণুর ছবি। কাছাকাছি অবস্থিত উজ্জ্বল বিন্দুগুলি সালফারের পরমাণু এবং অন্যগুলি মলিবডেনামের পরমাণু।

 একই ভাবে পরমাণু এমনকি ভারি অণুরও বিবর্তন ধর্মের প্রমাণ পাওয়া গেছে। অর্থাৎ একটা আশ্চর্য ঘটনার প্রমাণ পাওয়া গেল। সব কণারই তরঙ্গ ধর্ম আছে এবং তরঙ্গদৈর্ঘ্য হয় কণার ভরবেগের ব্যস্তানুপাতিক। সুতরাং ভারি কণার তরঙ্গদৈর্ঘ্য খুবই ছোট হবে, তাই পরীক্ষায় দেখা কঠিন। আবার এটাও দেখা গেল যে যখন তরঙ্গ ধর্মের প্রকাশ পায়, তখন তরঙ্গ সর্বত্র ছড়িয়ে পড়ে, তাই কণা ধর্ম আর দেখা যায় না [৩ (ক) নং ছবি]। আবার যখন বিভিন্ন তরঙ্গদৈর্ঘ্য বা ভরবেগের তরঙ্গ মিলিত হয়ে তরঙ্গের স্থানীয়করণ হয়ে যায়, তখন কণাধর্মের প্রকাশ পায় [৩(খ) নং ছবি]।

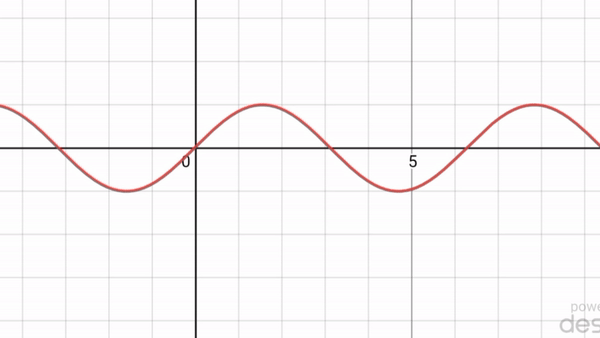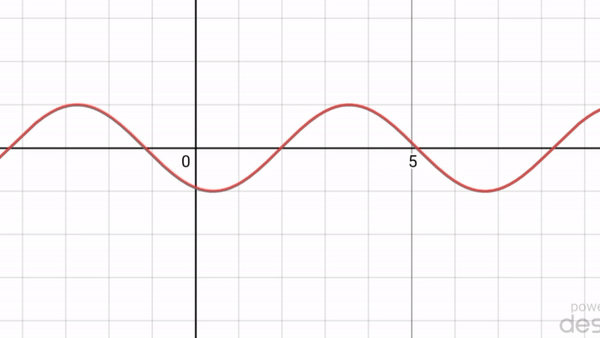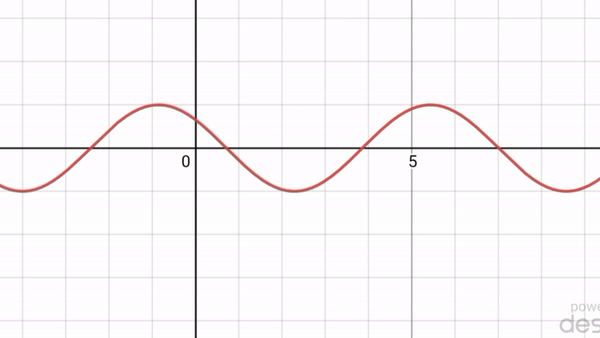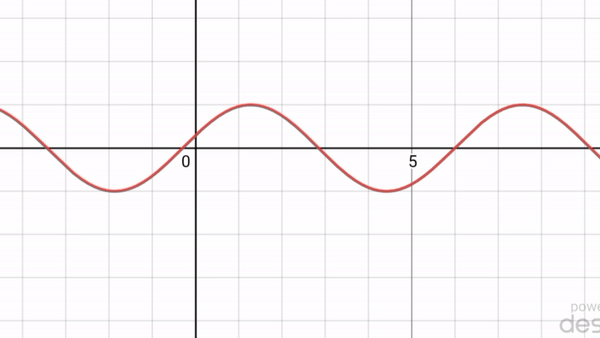
৩ (ক) নং ছবি :  নির্দিষ্ট তরঙ্গদৈর্ঘ্য এর তরঙ্গ। কোন অবস্থান সংক্রান্ত তথ্য নেই।

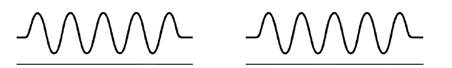
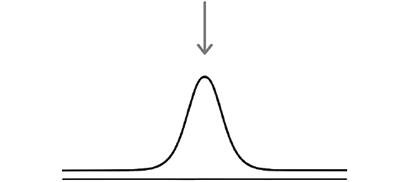
৩ (খ) নং ছবি :  বিভিন্ন তরঙ্গদৈর্ঘ্য বা ভরবেগের তরঙ্গ মিলিত হলে তাদের স্থানীয়করণ হয় এবং কণাধর্ম প্রকট পায়।  

প্রায় একই সময়ে আরও একটি আশ্চর্যজনক ঘটনা দেখা গেল। যে কোন মৌলকে বাষ্পীভূত করে তার বর্ণালী পরীক্ষা করলে দেখা যায় যে কিছু নির্দিষ্ট কম্পাঙ্কের আলো বেরোচ্ছে, সব কম্পাঙ্কের আলো তার থেকে আসছে না। যেমন হাইড্রোজেনের দৃশ্যমান বর্ণালীতে কেবলমাত্র লাল, নীল, ঘন নীল ও বেগুনী কম্পাঙ্ক দেখা যায় (৪ নং ছবি)। যেহেতু আলো সেই মৌলের পরমাণু থেকে বেরোয়, এর অর্থ দাঁড়ায় মৌলের পরমাণু কেবলমাত্র কিছু নির্দিষ্ট শক্তিস্তরে থাকতে পারে। এও তো আমাদের সাধারণ অভিজ্ঞতার সাথে মেলে না। দৈনন্দিন  অভিজ্ঞতায় আমরা দেখি একটা বস্তুর শক্তি সন্তত ভাবে বদলায়, তা কেবলমাত্র কিছু নির্দিষ্ট শক্তিস্তরে যায় না।

৪ নং ছবি :  হাইড্রোজেনের দৃশ্যমান বর্ণালী।

বিংশ শতকের প্রথমার্ধে বিজ্ঞান এই রকম একটা সন্ধিস্থলে এসে দাঁড়ায়। চিরাচরিত বিশ্বাসের বিপরীতে গিয়ে দেখা যায় যে কণার তরঙ্গ ধর্ম আছে, তবে কণা ধর্ম ও তরঙ্গ ধর্ম এক সাথে প্রকট হয় না, এবং পরমাণু বা যে কোন কণা কেবলমাত্র কিছু নির্দিষ্ট শক্তিস্তরে থাকতে পারে। প্রাকৃতিক জগতের এই গভীর ধাঁধার সমাধান হিসাবে আজ থেকে একশো বছর আগে কোয়ান্টাম বিজ্ঞানের আবিষ্কার হয়।

১৯২৫ সালে জার্মান বিজ্ঞানী Heisenberg এই ধাঁধার সমাধানে এক অভিনব ধারণার উপস্থাপনা করেন। তিনি প্রশ্ন করেন কি ভাবে আমরা একটা কণার অবস্থান জানতে পারি? ধরা যাক X-অক্ষ বরাবর কণাটির অবস্থান জানতে চাই। তাহলে X-অক্ষ বরাবর কোন আলোক রশ্মি বা যে কোন তড়িৎচুম্বকীয় তরঙ্গ বা অন্য কিছু নিক্ষেপ করতে হবে, যা ওই কণা থেকে প্রতিফলিত হয়ে আমার কাছে এলে আমি কণাটির অবস্থান জানতে পারবো। কিন্তু এর ফলে কণাটি আর স্থির থাকবে না, সে গতিশীল হয়ে যাবে এবং X-অক্ষ বরাবর কণাটির একটা ভরবেগ এসে যাবে। সুতরাং কণাটির অবস্থানের পরিবর্তন না ঘটিয়ে এবং তার মধ্যে ভরবেগের সঞ্চার না করে, আমরা কণাটির উপর কোন পরিমাপ করতে পারছি না। একটা নির্দিষ্ট তরঙ্গদৈর্ঘ্য এর আলোর সাহায্যে একটা কণার অবস্থান নির্ণয় করলে, ওই তরঙ্গদৈর্ঘ্য এর চেয়ে বেশি সূক্ষ্মতায় অবস্থান নির্ণয় করা যায় না এবং আলোর অভিঘাতে কণাটির ভরবেগ বদলে যায়। এর থেকে ১৯২৫ সালে Heisenberg বলেন যে একটা কণার X-অক্ষ (বা যে কোন অক্ষ) বরাবর অবস্থান নির্ণয়ের অনিশ্চয়তা এবং ওই একই অক্ষ বরাবর কণাটির ভরবেগের উপাংশ নির্ণয়ের অনিশ্চয়তার গুণফল একটা ধ্রুবকের (প্ল্যাঙ্কের ধ্রুবক) চেয়ে কখনো কম হতে পারে না। একে  Heisenberg এর অনিশ্চয়তার নীতি  বলে। অর্থাৎ একটা কণার অবস্থানের নিশ্চয়তা বাড়ালে তার ভরবেগ অনিশ্চিত হয়ে যাবে, আবার তার ভরবেগের নিশ্চয়তা বাড়ালে তার অবস্থান অনিশ্চিত হয়ে যায়। ব্যবহারিক এককে প্ল্যাঙ্কের ধ্রুবকের মান খুবই কম, তাই বড় বস্তুর ক্ষেত্রে এই অনিশ্চয়তার নীতির প্রভাব ধর্তব্যের মধ্যে নয়। যেমন একটা পাথরের উপর আলো ফেলে তার অবস্থান জানলে, পাথরটি প্রায় স্থিরই থাকে। কিন্তু একটা ক্ষুদ্র জলকণার উপর জোরালো আলো ফেললে, সেটি ঝাঁকুনি খায়। কল্পনার পরীক্ষায় (Thought experiment) একটা ইলেকট্রনের উপর আলো ফেললে, তার অবস্থান ও ভরবেগের পরিবর্তনকে অবহেলা করা যায় না।

একটা কণার অবস্থান নির্ণয় করতে গেলে যে তাকে বিচলিত করতে হয়, এটা কিন্তু অনেক আগেও জানা ছিল। তা সত্বেও আমরা তো একটা কণা বা ইলেকট্রনের যে কোন মুহূর্তে একটা নির্দিষ্ট অবস্থান ও ভরবেগের কল্পনা করতে পারি এবং তার ভিত্তিতেই নিউটনের বলবিদ্যা ও সনাতনী পদার্থ বিজ্ঞান গড়ে উঠেছিল। যে নতুন কথা Heisenberg বললেন, তা হল কোন মুহূর্তে একটা কণার সুনির্দিষ্ট অবস্থান ও ভরবেগের শুধু কল্পনা করলেই, তা বাস্তব হয় না। যদি কোনভাবে কণাটির সুনির্দিষ্ট অবস্থান ও ভরবেগের একই সাথে পরিমাপ করা যেত, তাহলেই তাদের যুগ্ম অস্তিত্ব বাস্তব হত। কিন্তু কোন Thought experiment করেও একটা কণার অবস্থান ও ভরবেগের একই সাথে সুনির্দিষ্ট পরিমাপ করা যায় না। কাজেই বাস্তবে তাদের যুগ্ম অস্তিত্ব নেই। অর্থাৎ যা পরিমাপ করা যায় না, তার কোন বাস্তব অস্তিত্ব নেই।

Heisenberg এর অনিশ্চয়তার নীতির মধ্যে স্বাভাবিকভাবেই কণার তরঙ্গধর্ম ও কণাধর্ম একত্রে নিহিত আছে। যদি কণার ভরবেগ সুনিশ্চিত করি, তাহলে তার অবস্থান পুরপুরি অনিশ্চিত হয়ে যাবে, অর্থাৎ তরঙ্গধর্ম প্রকট হবে, কারণ তরঙ্গের একটা নির্দিষ্ট তরঙ্গদৈর্ঘ্য (যার অর্থ ভরবেগ) থাকে, কিন্তু কোন নির্দিষ্ট অবস্থান থাকে না [৩ (ক) নং ছবি]। অপরদিকে কণাটির অবস্থান নিশ্চিত করার অর্থ তার স্থানীয়করণ করা এবং তখন তাকে অসংখ্য ভরবেগ বা তরঙ্গদৈর্ঘ্যযুক্ত তরঙ্গের সমন্বয় বলে ভাবা যায় [৩ (খ) নং ছবি]। সুতরাং অবস্থান নিশ্চিত করে স্থানীয়করণ করলে কণা ধর্ম প্রকট পায় এবং তখন সে অসংখ্য ভরবেগযুক্ত তরঙ্গের সমন্বয়, তাই তার ভরবেগ সম্পূর্ণ অনিশ্চিত। অতএব Heisenberg এর অনিশ্চয়তার নীতি আমাদের বলছে যে কণার তরঙ্গধর্ম আছে, কিন্তু কণাধর্ম ও তরঙ্গধর্ম একই সাথে কখনো প্রকট হতে পারে না।  

পরমাণুর যে কেবলমাত্র বিশেষ কিছু শক্তিস্তরে থাকতে পারে , তাও এই অনিশ্চয়তার নীতি থেকে বোঝা যায়। পরমাণুর কেন্দ্রে ধনাত্মক তড়িৎযুক্ত অতি ক্ষুদ্র নিউক্লিয়াস থাকে এবং তার চারিদিকে থাকে ঋণাত্মক তড়িৎযুক্ত ইলেকট্রনেরা। নিউটনের গতিবিদ্যা ও নিউক্লিয়াস এবং ইলেকট্রনের মধ্যে কুলম্ব আকর্ষণ ধরলে, ইলেকট্রন যে কোন শক্তি নিয়ে যে কোন কক্ষপথে থাকতে পারে। কিন্তু Heisenberg এর অনিশ্চয়তার নীতি অনুযায়ী, যদি ইলেকট্রন অতি ক্ষুদ্র বিন্দুবৎ নিউক্লিয়াসের খুব কাছে বা উপরে এসে পড়ে, তাহলে তার অবস্থানের অনিশ্চয়তা খুব কমে যাবে  এবং তার ফলে ভরবেগের অনিশ্চয়তা বিপুল হবে। তার ফলে ইলেকট্রনের গতিশক্তির অনিশ্চয়তা অনেক বেশি হবে এবং উচ্চ গতিশক্তির কারণে ইলেকট্রন নিউক্লিয়াসের থেকে দূরে চলে যাবে। কাজেই পরমাণুর ইলেকট্রনরা নিউক্লিয়াসের উপর পড়ে যাবে না এবং পরমাণুর একটা গঠন থাকবে। সুতরাং  ইলেকট্রনের ভরবেগ বা শক্তির অনিশ্চয়তা বিপুল হতে পারে না, অর্থাৎ ইলেকট্রনের যে কোন ভরবেগ বা শক্তি থাকা সম্ভব নয়। নিউক্লিয়াস ও ইলেকট্রনের মধ্যে ক্রিয়াশীল আকর্ষণী বলকে একটা বিভব কূপ হিসাবে মডেল করা যায় এবং তার মধ্যে ইলেকট্রন যে কোন স্থানে থাকতে পারে । অর্থাৎ ভাবা যেতে পারে যেন ইলেকট্রন ওই বিভব কূপের মধ্যে স্থাণু তরঙ্গ হিসাবে আছে এবং যে শক্তিস্তরগুলি কূপের মধ্যে অনুনাদের (resonance) সৃষ্টি করবে, কেবলমাত্র সেই শক্তিস্তরগুলি প্রাধান্য পাবে। যে  শক্তিস্তরগুলি অনুনাদ সৃষ্টি করতে পারে না, তাদের প্রাধান্য বা থাকার সম্ভাবনা অনেক কম হবে। কাজেই অনিশ্চয়তার নীতি ব্যবহার করে আমরা বুঝতে পারলাম কেন পরমাণুর শক্তিস্তর সন্তত নয় এবং কিছু নির্দিষ্ট সংখ্যক শক্তিস্তর (যারা বিভব কূপের মধ্যে অনুনাদ সৃষ্টি করে) শুধু তাদেরই দেখা যায়।

Heisenberg এর অনিশ্চয়তার নীতি থেকে জানলাম যে কোন কণার একই সাথে অবস্থান ও ভরবেগ নির্দিষ্টভাবে জানা যায় না। তাহলে কি নির্দিষ্টভাবে জানা যায়? ১৯২৬ সালে অস্ট্রিয়ার বিজ্ঞানী Erwin Schrödinger বলেন যে প্রতিটি  কণার সাথেই একটা তরঙ্গ অপেক্ষক (যা কণাটির অবস্থান ও সময়ের অপেক্ষক) যুক্ত আছে এবং তা একটা সুনির্দিষ্ট তরঙ্গ সমীকরণ মেনে চলে। এই তরঙ্গ অপেক্ষক সুনির্দিষ্টভাবে জানা সম্ভব এবং এর বর্গ কোন নির্দিষ্ট সময়ে কোন নির্দিষ্ট অবস্থানে কণাটির থাকার সম্ভাবনা বোঝায়। এই তরঙ্গ অপেক্ষক  এবং Schrödinger এর তরঙ্গ সমীকরণ ব্যবহার করেই কোয়ান্টাম মেকানিক্স গড়ে উঠেছে। কাজেই কোয়ান্টাম মেকানিক্স ব্যবহার করে আমরা কেবলমাত্র কোন নির্দিষ্ট সময়ে কণাটির কোন নির্দিষ্ট অবস্থানে থাকার সম্ভাবনা নির্ণয় করতে পারি।

১৯২৯ সালে H. P. Robertson কোয়ান্টাম মেকানিক্সের তরঙ্গ অপেক্ষকের ধারণা ব্যবহার করে দেখান যে কোয়ান্টাম গণনার মধ্যে স্বাভাবিকভাবেই একটা কণার অবস্থান ও ভরবেগের অন্তর্নিহিত অনিশ্চয়তা নিহিত আছে। অর্থাৎ কোন পরিমাপ না করে, কেবলমাত্র তাত্ত্বিক গণনা থেকে বলা যায় যে একটা কণার X-অবস্থানের প্রমাণ বিচ্যুতি (standard deviation) ও ভরবেগের X-উপাংশের প্রমাণ বিচ্যুতির গুণফল প্ল্যাঙ্কের ধ্রুবক ভাগ ৪π (π বৃত্তের পরিধি ও ব্যাসের ভাগফল) এর চেয়ে সর্বদাই বড় হবে। কোন রকম পরিমাপবিহীন এই তাত্ত্বিক গণনার ফল সর্বদাই সঠিক এবং এর কোন সীমাবদ্ধতা এখনো অবধি জানা নেই।

অপরদিকে Heisenberg এর পরিমাপভিত্তিক উপস্থাপনায় যে বলা হয়েছিল একটা কণার অবস্থান ও ভরবেগের পরিমাপভিত্তিক অনিশ্চয়তার গুণফল প্ল্যাঙ্কের ধ্রুবকের চেয়ে সর্বদা বড় হবে, তা সবক্ষেত্রে সঠিক নাও হতে পারে। যেমন বলা হয়েছিল যে একটা কণার অবস্থান নির্ণয়ের জন্য বাইরে থেকে আলো ফেলতে হবে এবং তার জন্য অবশ্যই কণাটির ভরবেগের পরিবর্তন হবে। এখন ধরা যাক কণাটি একটি পরমাণু। তাহলে পরমাণুর থেকে আলোক কণা বেরিয়েও পরমাণুটির অবস্থানের জানান দিতে পারে। তবে সেক্ষেত্রেও ভরবেগ সংরক্ষণের জন্য পরমাণুটি আলোক কণা নির্গমনের বিপরীতদিকে ভরবেগ পাবে, অর্থাৎ পরমাণুটি বিচলিত হবে এবং Heisenberg এর উপস্থাপনা সঠিক থাকবে। এখন ধরা যাক, পরমাণুটি থেকে প্রায় একই সময়ে প্রায় একই কম্পাঙ্কের দুটি আলোক কণা পরস্পরের বিপরীত দিকে নির্গত হল। এই দুটি আলোককণার গতিপথ সনাক্ত করে পরমাণুর অবস্থান নির্ণয় করা যায়, কিন্তু এক্ষেত্রে পরমাণুটি কোন ভরবেগ পাবে না, কারণ সমান কম্পাঙ্কের দুটি বিপরীতদিকে ধাবমান আলোককণার মোট ভরবেগ শূন্য হয়। অতএব পরমাণুটিকে বিচলিত না করেই তার অবস্থান জানা সম্ভব হচ্ছে, অর্থাৎ অবস্থান নির্ণয়ের অনিশ্চয়তা খুব কম হচ্ছে, কিন্তু ভরবেগের অনিশ্চয়তা বাড়ছে না । সুতরাং  যে সংকেতের সাহায্যে কণাটির অবস্থান নির্ণয় করা হচ্ছে, তা যদি কণাটি থেকে নিরপেক্ষ হয় (যেমন বাইরে থেকে আলো ফেলে কণার অবস্থান নির্ণয় করা), তাহলে Heisenberg এর পরিমাপভিত্তিক উপস্থাপনা সঠিক, অন্যথায় নয়।  

তবে পরিমাপের সাথে কোয়ান্টাম অনিশ্চয়তার অবশ্যই ঘনিষ্ঠ সম্পর্ক আছে, তা নইলে এই অনিশ্চয়তার নীতির ব্যবহারিক প্রয়োগ সম্ভব হবে না, তাত্ত্বিকভাবেও ব্যাপারটা জানা প্রয়োজন। ২০০৬ সালে জাপানী বিজ্ঞানী Masanao Ozawa এর তাত্ত্বিক কাজ এবং ২০১২ সালে J. Erhart ও Lee A. Rozema এবং অন্যান্যদের পরীক্ষামূলক কাজ থেকে পরিমাপভিত্তিক কোয়ান্টাম অনিশ্চয়তার সঠিক ফর্মুলাটি জানা যায়। দেখা যায় যে Heisenberg এর প্রস্তাবিত কণার অবস্থানের পরিমাপভিত্তিক অনিশ্চয়তা ও ভরবেগের পরিমাপভিত্তিক অনিশ্চয়তার গুণফল রাশিটির অবশ্যই অবদান আছে, তবে তাছাড়াও অবস্থান নির্ণয়ের সংকেত ও কণার মধ্যে সম্পর্ক থাকলে আরও দুটি রাশি আসে এবং এই তিনটি রাশির যোগফল প্ল্যাঙ্কের ধ্রুবক ভাগ ৪π এর চেয়ে সর্বদাই বড় হবে। এটাই হচ্ছে পরিমাপভিত্তিক কোয়ান্টাম অনিশ্চয়তার সাধারণ সূত্র।

এইবার আধুনিক যোগাযোগ ব্যবস্থায় কোয়ান্টাম অনিশ্চয়তার নীতির একটা ব্যবহারের কথা বলে শেষ করবো। আজকের দিনে গুপ্ত লিপি প্রেরণ যোগাযোগ ব্যবস্থার একটা গুরুত্বপূর্ণ অঙ্গ। ব্যাংকের লেনদেন হয় One Time Password (OTP) এর মাধ্যমে। এই OTP যেন অবশ্যই কেবলমাত্র প্রেরক ও গ্রাহকের মধ্যে থাকে, আর কেউ যেন জানতে না পারে। সামরিক ও নানান জাতীয় ক্ষেত্রে গুপ্ত লিপি প্রেরণ করার দরকার পড়ে ও তার গোপনীয়তা বজায় রাখা প্রয়োজন হয়। প্রেরিত গুপ্তলিপির গোপনীয়তা সর্বদাই OTP বা কোন গোপন চাবিকাঠির মাধ্যমে রক্ষা করা হয়। সাধারণভাবে প্রেরিত OTP বা গোপন চাবিকাঠি প্রেরক ও গ্রাহকের অজ্ঞাতে জেনে নেওয়া সম্ভব। OTP বা গোপন চাবিকাঠির interception অর্থাৎ মাঝপথে জেনে নেওয়া আটকানো অন্তত তাত্ত্বিকভাবে সম্ভব নয়। কাজেই ধরে নিতে হবে যে গোপন চাবিকাঠি মাঝ পথে জেনে নেওয়া যেতে পারে। তবে কোয়ান্টাম অনিশ্চয়তার নীতিকে ব্যবহার করে এটা নিশ্চিত করা যায় যে যদি কেউ মাঝপথে OTP বা গোপন চাবিকাঠি জেনে নেয়, তাহলে প্রেরক ও গ্রাহক অবশ্যই টের পাবে যে কেউ তাদের গোপন চাবিকাঠি জেনে ফেলেছে। কিভাবে এই কাজ করা সম্ভব?

OTP বা গোপন চাবিকাঠি পাঠান হয় ০ ও ১ দিয়ে গঠিত দ্বিনিধানী সংখ্যার মাধ্যমে। সনাতনী পদ্ধতিতে নিম্ন ও উচ্চ বৈদ্যুতিক বিভব দ্বারা ০ ও ১ কে বোঝানো হয়। কোয়ান্টাম পদ্ধতিতে কোয়ান্টাম বিট দিয়ে ০ ও ১ কে বোঝানো হয়। তারপর এই কোয়ান্টাম বিট পাঠানো হয়। কেউ মাঝপথে এই কোয়ান্টাম বিট পড়ে নিলে, কোয়ান্টাম অনিশ্চয়তার অমোঘ নিয়মে বিট বিকৃত হয়ে যাবে এবং চ্যানেলে আওয়াজ উঠবে। কাজেই প্রেরক ও গ্রাহক জানতে পারবে যে কেউ লিপি পড়েছে। এটাই মূল নীতি।

কোয়ান্টাম বিট কি, সেটা একটু বুঝিয়ে বলা যাক। একটা মৌলের ক্ষুদ্রতম কণা যেমন পরমাণু, তেমনি একটা নির্দিষ্ট কম্পাঙ্কের আলোর নুন্যতম শক্তিগুচ্ছ হচ্ছে তার আলোককণা বা ফোটন। একটা আলোককণার শক্তি হচ্ছে প্ল্যাঙ্কের ধ্রুবক গুণ তার কম্পাঙ্ক। আলোককণার সাথে তড়িৎচুম্বকীয় তরঙ্গ যুক্ত থাকে, অর্থাৎ আন্দোলিত বৈদ্যুতিক ও চৌম্বক ক্ষেত্র যুক্ত থাকে। ধরা যাক Z-অক্ষ বরাবর আলোককণা যাচ্ছে , তাহলে X-Y তলে অবস্থিত এবং মূল বিন্দুর মধ্যে দিয়ে যাওয়া যে কোন সরলরেখা বরাবর  আন্দোলিত বৈদ্যুতিক ক্ষেত্র থাকতে পারে এবং তা আলোককণার ধ্রুবণের (polarization) দিক নির্দেশ করে। অতএব X-Y তলে অবস্থিত এবং মূল বিন্দুর মধ্যে দিয়ে যাওয়া যে কোন সরলরেখা বরাবর আলোককণাকে ধ্রুবিত (polarized) করা যায়। এইবার একটা প্রোটোকল ঠিক করতে হয়। একটা প্রচলিত প্রোটোকল অনুযায়ী আমরা ঠিক করলাম যে Z-অক্ষ বরাবর ধাবিত আলোককণাকে আমরা কেবলমাত্র  X-অক্ষ বা Y-অক্ষ বরাবর ধ্রুবিত করবো। X-অক্ষ বরাবর ধ্রুবিত আলোককণাকে o বিট ও Y-অক্ষ বরাবর ধ্রুবিত আলোককণাকে ১ বিট বললাম। এক্ষেত্রে আমরা বলি যে X/Y অক্ষ বেসিস স্টেটে কাজ করছি। আমরা +৪৫°/-৪৫° অক্ষ বেসিস স্টেট ব্যবহার করলে,  X-Y তলে মূল বিন্দুর মধ্যে দিয়ে X -অক্ষের সাথে +৪৫° কোণ করে যাওয়া সরলরেখা বরাবর ধ্রুবিত আলোককণাকে o বিট ও -৪৫° কোণ করে যাওয়া সরলরেখা বরাবর ধ্রুবিত আলোককণাকে ১ বিট বলবো। এক্ষেত্রে গুরুত্বপূর্ণ ব্যপার হচ্ছে একটি ধ্রুবিত আলোককণাকে কোয়ান্টাম বিট বলা হয়, অর্থাৎ গুপ্ত সংকেত অবশ্যই একটি একটি করে পাঠানো ধ্রুবিত আলোককণার মাধ্যমে পাঠাতে হবে, এক গুচ্ছ আলোককণা একটা কোয়ান্টাম বিট হবে না।

কোয়ান্টাম অনিশ্চয়তার নীতি অনুযায়ী একটা আলোককণার ধ্রুবণের দিক একই সাথে দুটি ভিন্ন বেসিস স্টেটে বলা যায় না। যদি X/Y অক্ষ বেসিস স্টেটে একটা আলোককণার ধ্রুবণের দিক X-অক্ষ বরাবর হয়, তাহলে +৪৫° /-৪৫° অক্ষ বেসিস স্টেটে তার ধ্রুবণের দিক সম্পূর্ণ অনিশ্চিত হয়ে যায়, অর্থাৎ +৪৫° লাইন বরাবর বা -৪৫° লাইন  বরাবর ধ্রুবিত দেখার সম্ভাবনা সমান সমান হয়ে যায়। সুতরাং X/Y অক্ষ বেসিস স্টেটে কোয়ান্টাম বিট ১, +৪৫° /-৪৫° অক্ষ বেসিস স্টেটে সমান সম্ভাবনায় ০ বা ১ যে কোন মান নিতে পারে।

এইবার ধরা যাক প্রেরক এলিস একটা একটা করে ধ্রুবিত আলোককণার মাধ্যমে গ্রাহক ববকে গুপ্ত চাবিকাঠি পাঠাচ্ছে। এলিস কখনো X/Y অক্ষ বেসিস আবার কখনো +৪৫°/-৪৫° অক্ষ বেসিস স্টেট ব্যবহার করে কোয়ান্টাম বিট পাঠাচ্ছে। ধরা যাক ইভ মাঝ রাস্তায় আলোককণাগুলিকে ধরে ফেলছে এবং কোন বিট (০ না ১ ) তা পড়ছে ও তার নির্ণয় অনুযায়ী আবার সেই কোয়ান্টাম বিট ববকে পাঠিয়ে দিচ্ছে। বব বা ইভ কেউই জানে না কখন কোন বেসিস স্টেট ব্যবহার করে এলিস কোয়ান্টাম বিট পাঠাচ্ছে। কাজেই তারা আন্দাজে যা খুশি (random) বেসিস স্টেট ব্যবহার করে কোয়ান্টাম বিট পড়ছে এবং যখনই ভুল বেসিস ব্যবহার করছে, তখনই এলোমেলো (random) বিট পড়ছে। গুপ্ত লিপি পাঠানোর পরে এলিস পাবলিক চ্যানেলে অর্থাৎ সর্বসমক্ষে ববকে জানিয়ে দিল যে সে কখন কোন বেসিস স্টেট ব্যবহার করেছে, তবে অবশ্যই ০ না ১ কোন কোয়ান্টাম বিট পাঠিয়েছিল, সেটা জানাচ্ছে না। বেসিস স্টেট জানার পরে বব তার ব্যবহৃত ভুল বেসিস স্টেট এর বিটগুলো বাদ দিয়ে দিল এবং সঠিক বেসিস স্টেটগুলোর ভিত্তিতে কেবলমাত্র সঠিক বিটগুলো রাখলো। এইবার বব সঠিক বিটগুলোর অল্প কিছু অংশ নিয়ে পাবলিক চ্যানেলে এলিসের সাথে তার পাঠানো বিটগুলোর তুলনা করলো। অবশ্যই ১০০% মিল হওয়া উচিত, কারণ দুইজনেই একই বেসিস ব্যবহার করেছে। কিন্তু যদি মাঝপথে ইভ বিটগুলো পড়ে নিয়ে আবার পাঠিয়ে থাকে, তাহলে বব ও এলিসের বিটগুলোর মধ্যে   ১০০% মিল পাওয়া যাবে না। ইভও আন্দাজে বেসিস ঠিক করে বিট পড়েছিল। কাজেই ইভের বেসিস গড়ে অর্ধেক সময়ে ভুল হবে এবং সে গড়ে ২৫% ভুল বিট ববকে পাঠাবে। কাজেই বব  ও এলিসের বিটগুলোর তুলনায় গরমিল ধরা পড়বে এবং তারা বুঝতে পারবে যে কেউ মাঝ পথে তাদের পাঠানো বিটগুলো পড়েছে। কোয়ান্টাম অনিশ্চয়তার অমোঘ নিয়মে ইভ কোন ভাবেই তার উপস্থিতি লুকোতে পারবে না এবং বব ও এলিস ইভের অস্তিত্ব টের পাবে।

প্রকৃতির এক গভীর ধাঁধার সমাধান হিসাবে কিভাবে কোয়ান্টাম অনিশ্চয়তা ও কোয়ান্টাম বিজ্ঞান এসেছিল, তা নিয়ে আলোচনা করলাম। বিমূর্ত ও দার্শনিক কোয়ান্টাম অনিশ্চয়তার নীতির যোগাযোগ ব্যবস্থায় একটা বাস্তব প্রয়োগের উদাহরণ দিলাম। এই রকম আরও অনেক প্রয়োগ আছে এবং আরও অনেক অজানা প্রয়োগ ও ব্যবহার তোমরা ভবিষ্যতে আবিষ্কার করবে।