কলমে এলেবেলে চিরশ্রী ~

কোয়ান্টাম মেকানিক্সের পেপার। পরীক্ষা চলছে বেলা স্যারের নিশ্ছিদ্র প্রহরায় (যাদের এখনো আলাপ হয়নি বেলা স্যারের সাথে, তারা একবার আগের পর্বে ঘুরে আসুন)। হঠাৎ চোখ চলে গেল একদম শেষ বেঞ্চে বসা মেয়েটার দিকে। তার খাতার পাতায় খসখস করে হেঁটে বেড়াচ্ছে নীলরঙা বলপেন। কিন্তু কী অদ্ভুত! চোখটা ঠিক খাতার দিকে নয়, বামদিকে হেলে আছে। নিজের মোবাইলটা হাতে নিয়ে কী যেন একটা দেখে নিলেন বেলা স্যার। “মা রে! পরীক্ষার খাতায় লিখতে লিখতে চ্যাটে অনলাইন থাকার উপায়গুলো একটু বলবি?”— মেয়েটার পাশে দাঁড়িয়ে ফিসফিসিয়ে বললেন স্যার। “কি বলছেন স্যার, আমি তো কিছুই বুঝছি না! আ-আ-আ-মি অনলাইন? আমি কেন মোবাইল লুকিয়ে চ্যাট করব!”— চোখেমুখে বিস্ময়ের ভাব এনে জবাব দিল মেয়েটা। মুখটা ব্যাজার করে বেলা স্যার বলে উঠলেন— “তোরা হলি সাক্ষাৎ প্রকৃতি। সাহিত্য, পুরাণে মাদার নেচারের সাথে তোদের তুলনা করা হয়। এসব লুকোছাপা কি তোদের সাজে রে মা?” এসব শুনে খানিকটা অনুতপ্তই বোধ করল মেয়েটা। এক মুহুর্তের জন্য ভাবল, সত্যিটা বলেই দেবে স্যারকে, কিন্তু পরক্ষণেই দুষ্টু বুদ্ধি খেলে গেল মাথায়। বলে উঠল— “ওটাই সমস্যা জানেন! আপনি তো আমাদের প্রকৃতি-স্বরূপা বলে দিলেন। কিন্তু এই প্রকৃতি জিনিসটা খুব একটা সুবিধার নয় তো! গোপন কথা তার পেট থেকে বের করা কিন্তু শুধু মুশকিলই নয়, অসম্ভবও।” মুখে রাগের অভিব্যক্তি থাকলেও, মনে মনে খানিকটা হেসে নিলেন বেলা স্যার। সত্যিই তো! প্রকৃতিকে অণুবীক্ষণে ফেললে যে অণু, পরমাণুর সূক্ষ্মাতিসূক্ষ্ম দুনিয়ার হদিশ পাওয়া যায়, তা তো গোপনীয়তায় মোড়া! তবে বেলা স্যারের কাছে এত ভাবার সময় নেই এখন, তাই ওনার ভাবনার সূত্র ধরে আসুন আমরাই প্রবেশ করি কোয়ান্টামের জগতে।
ধরুন আপনি একটা ইলেকট্রনকে ধরে ভাবলেন, এইবার এর অবস্থান আর ভরবেগ একসাথেই মেপে ফেলবেন। কিন্তু হায়! সে একই সঙ্গে দুটো তথ্য নির্ভুলভাবে কিছুতেই দেবে না আপনাকে; সেই হেইজেনবার্গের অনিশ্চয়তা নীতির গল্প বলেছিলাম না (কোয়ান্টামের কড়চা: “হাতে রইল পেন্সিল”)! শুধু কি তাই, আপনি হয়তো ভাবলেন চুপচাপ মাপজোখ করে মানে মানে কেটে পড়বেন, কেউ জানতেও পারবে না, সে গুড়েও বালি। সেই শ্রাওডিংগারের বাক্সবন্দি বেড়ালের গল্পটা এতক্ষণে নিশ্চয়ই পড়ে ফেলেছেন, যেখানে বাক্সের ভেতরে একই সঙ্গে বেড়ালটা জীবিত ও মৃত— দুটো অবস্থার উপরিপাতন (সুপার-ইমপোসিশন) হিসেবে বসবাস করছিল। যেই না একবার আপনি দেখে ফেললেন তাকে, ওমনি বেড়ালটা যে কোন একটা অবস্থায় চলে গেল। আপনি দেখলেন একটা জীবিত অথবা মৃত বেড়ালকে। অন্য সম্ভাবনাটাকে নষ্ট করে দিল আপনার দেখে ফেলাটাই। তাহলে? আণুবীক্ষণিক জগতের প্রকৃতিই কি আমাদের জানার পথে কাঁটা হয়ে দাঁড়াবে?
যদি কোয়ান্টাম দুনিয়ার এই প্রতিবন্ধকতাকেই তথ্য গোপন রাখার অস্ত্র হিসেবে ব্যবহার করা যায়?
যদি কোয়ান্টাম দুনিয়ার এই প্রতিবন্ধকতাকেই তথ্য গোপন রাখার অস্ত্র হিসেবে ব্যবহার করা যায়? কোয়ান্টাম তত্ত্ব ব্যবহার করে যদি তৈরি করা যায় এমন একটি চাবি, যাকে যেই না আপনি আড়ি পেতে দেখতে গেলেন, সে নিজেই গেল বদলে! উপরন্তু আপনিও পড়ে গেলেন ধরা।
মনে করুন, অ্যালিস আর বব দুই বন্ধু। অ্যালিস কিছু খুব গোপনীয় তথ্য পাঠাতে চায় ববকে। কিন্তু মাঝ রাস্তায় আড়ি পেতে বসে আছে ইভ। অ্যালিস আর বব ঠিক করল, তারা এমন একটা কোয়ান্টাম-চাবি তৈরি করবে, যা হবে ১) দু’জনের যৌথ উদ্যোগে তৈরি, এবং ২) মাত্র একবার ব্যবহারের যোগ্য (ওয়ান টাইম প্যাড)। প্রথমে তারা নিজেদের তথ্য আদান-প্রদান করার জন্য দুটো রাস্তা বানালো। একটা রাস্তা ক্লাসিকাল, অন্যটা কোয়ান্টাম। একটু পরে আমরাও ওদের সাথে এই দুটো রাস্তা ধরে হাঁটব, তবে তার আগে একবার চলুন ঘুরে আসি সনাতন গণকের অফিসে।
আমরা জানি, সনাতন গণক বা ক্লাসিকাল কম্পিউটারকে আমরা যাই লিখতে, পড়তে, গুনতে বা করতে দিই না কেন, সে সেগুলোকে প্রথমে ভেঙে নেয় ‘০’ এবং ‘১’— এই দু’টি অঙ্কে। ‘০’ আর ‘১’ অনেকটা সুইচের মতই, যা অন ও অফ, বা বলা ভালো তড়িৎ বর্তনীর উঁচু ও নিচু বিভবকে বোঝায়। তার যাবতীয় হিসেব ওই ‘০’ আর ‘১’-কে নিয়েই। তার বাইরে একবর্ণও বোঝে না সে। কোয়ান্টাম প্রযুক্তিতেও আমাদের দরকার এরকমই কিছু ‘০’ এবং ‘১’-এর। সাধারণত পরমাণু এবং ফোটন জাতীয় আণুবীক্ষণিক কণাকে ব্যবহার করে ‘০’ এবং ‘১’-কে তৈরি করার বেশ কিছু উপায় আছে (‘আলো, কোয়ান্টাম, আর কম্পিউটার’ লেখাটি পড়ে দেখতে পারেন)। আমাদের আজকের গল্পের অ্যালিস-ববের কোয়ান্টাম-চাবি বানাতে আমরা সাহায্য নেব ফোটন কণার, যা আদতে তড়িৎ-চুম্বকীয় তরঙ্গ বা আলোর কণা-রূপ। চিনে নেব ফোটন কণার ‘১’ এবং ‘০’-কে।
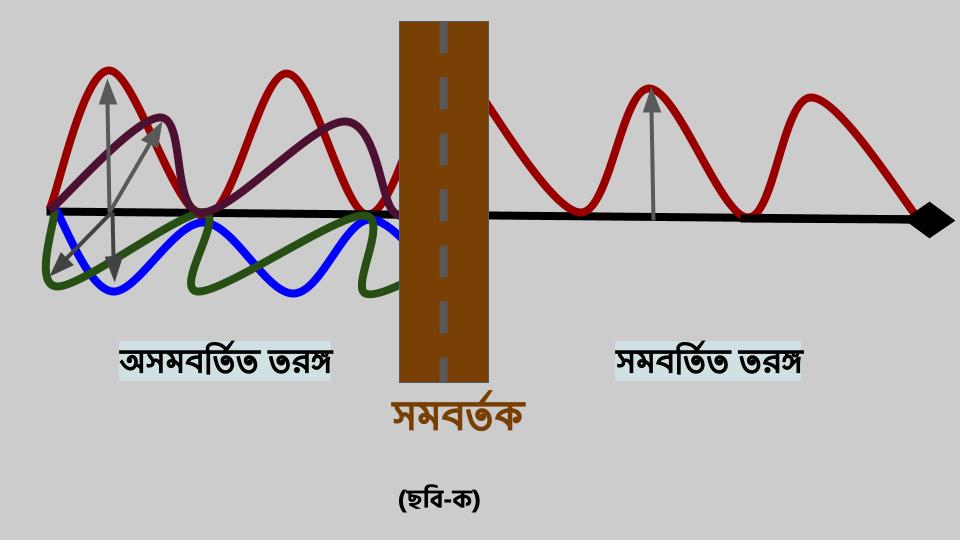
যে আলো বা তড়িৎ-চুম্বকীয় তরঙ্গ নিয়ে আমাদের কাজ কারবার, তার তড়িৎক্ষেত্রের অভিমুখটি থাকে তরঙ্গের চলনের অভিমুখের সাথে উলম্ব ভাবে। কিন্তু এই তড়িৎক্ষেত্রটি বাধ্য ছাত্রের মত একই অভিমুখে থাকে না, সে তরঙ্গের গতির সাথে থাকা উলম্বতলের যে কোন দিক বরাবর থাকতে পারে। ফলে এই ধরণের তির্যক তরঙ্গ (ট্রান্সভার্স ওয়েভ) একাধিক তলে স্পন্দনশীল অবস্থায় থাকে— এরকম তড়িৎ-চুম্বকীয় তরঙ্গকে বলে অসমবর্তিত (আনপোলারাইজড) তরঙ্গ (ছবি-ক)। এই অবাধ্য তরঙ্গকে যদি এমন কোন দরজা দিয়ে ঢুকতে বাধ্য করা যায়, যাতে তার তড়িৎক্ষেত্রের অভিমুখকে একটা দিক বা নিয়মে বেঁধে দেওয়া যায়, তাহলে এই নিয়ম মেনে চলা তরঙ্গটিকে বলা হয় সমবর্তিত (পোলারাইজ) তরঙ্গ, এবং এই দরজাটিকে বলা হয় সমবর্তক (পোলারাইজার)। তড়িৎ-চুম্বকীয় তরঙ্গের এই ধর্মটি তার কণা-স্বরূপ ফোটনের ঘূর্ণন (স্পিন) ধর্মটির সাথে তুলনীয়। একটি সমবর্তিত ফোটনের সরলরৈখিক (↑ ও →) অথবা তির্যক (↘ এবং ↗) অভিমুখ থাকতে পারে। একটা অসমবর্তিত ফোটনের অবস্থাকে আমরা এই সবগুলি অবস্থার উপরিপাতন (সুপার-ইমপোসিশন) হিসেবে ভাবতে পারি।
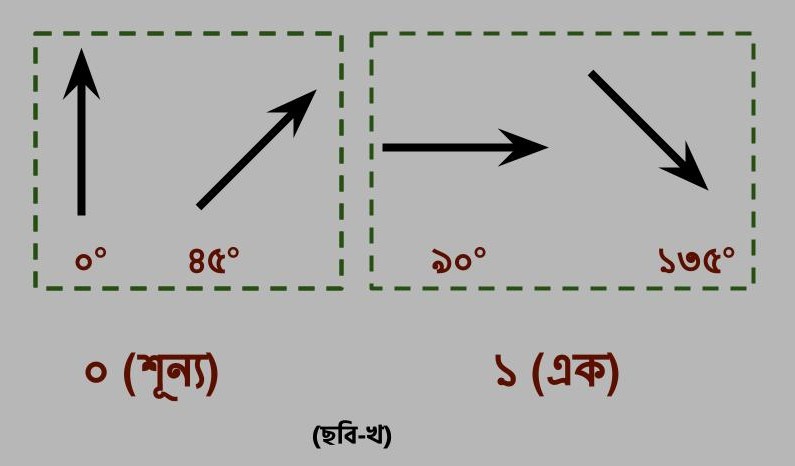
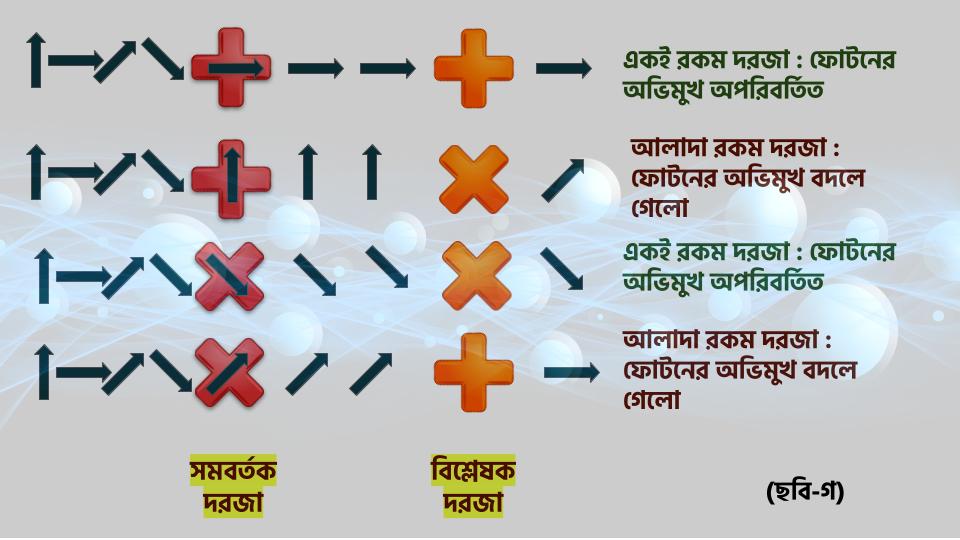
এবার ধরা যাক আমার কাছে দুটো দরজা আছে। একটা দেখতে যোগ (十) চিহ্নের মত, অন্যটা গুণ (X) চিহ্নের মত। এই দরজাগুলো এক একটা ছাঁকনি বা সমবর্তক, যাদের কাজ ফোটনগুলোকে একটা নির্দিষ্ট অভিমুখে যেতে বাধ্য করা। যেমন, (十)-এর মত দরজা দিয়ে ফোটনগুলো হয় ৯০ ডিগ্রী (→) অথবা ০ ডিগ্রী (↑) কোণে পার হতে পারে। আবার (X)-এর মত দরজাটা দিয়ে ঢুকতে গেলে তাকে হয় ৪৫ ডিগ্রী (↗) অথবা ১৩৫ ডিগ্রী (↘) কোণ করে পেরতে হবে (ছবি-গ)। এবার ধরা যাক ০ এবং ৪৫ ডিগ্রীতে হেলে থাকা ফোটনগুলোকে ‘০’, এবং ৯০ ও ১৩৫ ডিগ্রীতে হেলে থাকা ফোটনগুলোকে ‘১’ দিয়ে চিহ্নিত করা হল (ছবি-খ)। তবে যেটা সব থেকে আগ্রহের বিষয়, তা হল এই ‘০’ এবং ‘১’-এর সাথে ক্লাসিকাল কম্পিউটারের ‘০’ এবং ‘১’-এর একটা বিশেষ পার্থক্য আছে।
সহজভাবে বোঝার জন্য, এই ‘০’ এবং ‘১’ অবস্থাকে যদি আমরা দুটো রঙের মত ভাবি— লাল ও নীল, তাহলে বলা যায়, একটা ফোটন সবসময় এই দুটো রঙের মিশ্রণের মত থাকে। একটা সমবর্তকের দরজা দিয়ে যেতে বাধ্য করার অর্থ হল রঙের মিশ্রণ থেকে একটা নির্দিষ্ট রঙকে নির্বাচন করা। কোয়ান্টামের বিদঘুটে বৈশিষ্ট্যের জন্য, একটা রঙকে যতটা সঠিকভাবে বেছে নেওয়া হবে, অন্য রঙের সমস্ত খবরাখবর পাওয়ার সম্ভাবনা ততটাই কমে যাবে।
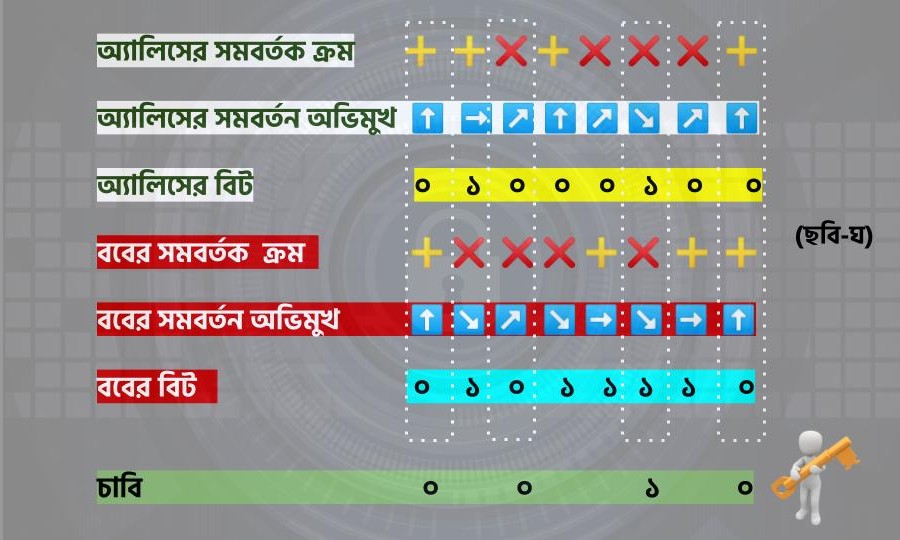
যাই হোক, আবার ফিরে আসা যাক অ্যালিস-ববের গল্পে। ধরা যাক, এক ঝাঁক অসমবর্তিত ফোটন কণা নিয়ে অ্যালিস শুরু করল চাবি তৈরির কাজ। সে নিজের ইচ্ছেমত (十) এবং (X) সমবর্তকের দরজা দিয়ে চার রকমের অভিমুখ-বিশিষ্ট সমবর্তিত ফোটন পাঠাতে শুরু করল ববকে, কোয়ান্টামের রাস্তা দিয়ে— আলোকীয় তন্তুর মাধ্যমে। তার কাছে রাখা নোট বইয়ে সে লিখে রাখল নিজের ব্যবহার করা দরজার ক্রম ও ফোটনের অভিমুখ। ধরা যাক অ্যালিস আটখানা ফোটন পাঠাল, নিচের ছবিতে দেওয়া ক্রমে (ছবি-ঘ)। ববকে সে জানালোই না ফোটনকে কোন ক্রমে পাঠানো হয়েছে।
ববের কাছে আবার আছে ফোটন ধরার কল— যার নাম বিশ্লেষক (অ্যানালাইজার)। সেগুলিও (十) এবং (X)-এর মত এক একখানা দরজা। ববও নিজের মর্জিমত পরপর আটখানা বিশ্লেষক-দরজা দিয়ে ফোটনগুলোকে ঢুকতে দিল। আবারও মনে করিয়ে দিই, বব কিন্তু এখনো জানে না, অ্যালিসের দরজার ক্রম। নিচের ছবিতে ববের দরজার ক্রমও দেওয়া আছে (ছবি-ঘ)।
হিসেবমত অ্যালিস ও বব একই রকম দরজা ব্যবহার করলে, বব ঠিক তথ্যটি সংগ্রহ করতে পারবে। ধরা যাক, অ্যালিস (十) দরজা দিয়ে একটা ০ ডিগ্রীর সমবর্তিত ফোটন (↑) পাঠাল। এখন বব যদি (十) দরজা ব্যবহার করে, সে ওই ফোটনটিকে ধরতে পারবে। অন্যদিকে, বব যদি (X) দরজার ব্যবহার করে, সেই দরজা দিয়ে ঢোকার সময় ফোটনের অভিমুখ যাবে বদলে (ছবি-গ)। কোয়ান্টামের ভাষায় বলতে গেলে, বব যেহেতু ভুল দরজা দিয়ে মাপছে, সে ওই দরজা বরাবর ফোটনের তির্যক অভিমুখটি (↘অথবা ↗) মাপতে বাধ্য হবে, যা ফোটনটির পূর্ববর্তী অভিমুখটিকে (↑) আর জানতে দেবে না (ছবি-গ)। তাহলে উপায়? এরকম সুরক্ষার অর্থটা কী, যা ববকেও পুরো তথ্য জানতে দিচ্ছে না! তাহলে?
বব এবার অ্যালিসকে ফোন করবে ক্লাসিকাল পথে। এই পথ খুব সুরক্ষিত না হলেও চলবে। বব অ্যালিসকে বলবে তার ব্যবহার করা বিশ্লেষকের ক্রম। অ্যালিস পরপর নিজের ব্যবহার করা সমবর্তকের ক্রমের সাথে তা মেলাতে থাকবে। যেগুলো মিলবে না, সেই ক্রমে থাকা সমবর্তক-বিশ্লেষকদ্বয়ের তথ্যকে বাতিল করে শুধুমাত্র সেই দরজাগুলোর পেছনে থাকা ফোটনের সংশ্লিষ্ট মান (০ বা ১) লিখে রাখা হবে, যারা একই রকম দরজা দিয়ে অ্যালিসের কাছ থেকে বেরিয়েছে ও ববের কাছে ঢুকেছে। নিচের ছবিটা দেখলে ব্যাপারটা পরিষ্কার বোঝা যাবে (ছবি-ঘ)। অ্যালিস-ববের নির্বাচিত দরজার পেছনে থাকা ‘০’ এবং ‘১’-কে ক্রমানুসারে সাজালে যে সংখ্যাটি পাওয়া যাবে, সেটাই হল কোয়ান্টাম-চাবি, বা পাসওয়ার্ড।
কিন্তু এত কাঠখড় পুড়িয়ে তৈরি করা কোয়ান্টামের চাবি যে মাঝ রাস্তায় আড়ি পেতে থাকা ইভ চুরি করতে পারবে না, সেটা কি হলফ করে বলা সম্ভব? দেখা যাক! ইভ মাঝ রাস্তায় ফোটনকে দেখতে চাইলে তাকেও ওই ফোটনগুলোকে ধরার জন্য কল বা বিশ্লেষক দরজা ব্যবহার করতে হবে। আর কোয়ান্টাম দুনিয়ায় নীরব দর্শক হওয়া তো সম্ভব নয়, তার মাপার প্রচেষ্টা বদলে দিতে পারে ফোটনের অভিমুখকেই। শুধু তাই নয়, অ্যালিস-বব নিজেদের মধ্যে ব্যবহার করা দরজার ক্রম মেলাতে গেলেই ধরা পড়ে যাবে ইভের কারচুপি, তাও আবার পাসওয়ার্ডটি বানানোর আগেই। এরকম হলে, অ্যালিস-বব আবার নতুন করে ফোটন পাঠানোর প্রক্রিয়াটি শুরু করবে। ইভের হাতে এক বান্ডিল অর্থহীন ফোটন ছাড়া আর কিছুই ধরা দেবে না।
কিন্তু এই পদ্ধতিতে তথ্য আদান-প্রদান করার সব থেকে বড় বাস্তবিক সমস্যা হল, সমবর্তিত ফোটনকে এক জায়গা থেকে অন্য জায়গায় স্থানান্তরিত করা। এই ফোটনের সমবর্তিত অভিমুখগুলো এতটাই স্পর্শকাতর যে, অতি সামান্য তাপমাত্রার হেরফের, বা অতি নগণ্য কোন বিশৃঙ্খলাও বদলে দিতে পারে ফোটনের অভিমুখ। এই প্রতিকূলতা কাটিয়ে ১৯৮৯ সালে ‘অ্যালিস’ নামের একটি কম্পিউটার থেকে ৩৬ সেন্টিমিটার দূরে রাখা ‘বব’ নামের একটি কম্পিউটারে প্রথম এই কোয়ান্টাম-চাবি ব্যবহার করে সুরক্ষিত তথ্য পাঠানো হয়। গত বছর (২০২০ সালে) প্রকাশিত একটি গবেষণায় দাবি করা হয়, উন্নততর প্রযুক্তির সাহায্যে ৫০৯ কিলোমিটার দূরত্বে থাকা দুটো কম্পিউটারের মধ্যে কোয়ান্টাম-চাবি ব্যবহার করে তথ্য পাঠানো সম্ভব। আপাতত এটুকু বলাই যায় যে, কোয়ান্টাম প্রযুক্তির রাস্তায় এখনো অনেকটা পথ হাঁটা বাকি।
পরের পর্বে আমরা হাঁটব আরো একটা কোয়ান্টামের পথ ধরে, যে পথ কল্পবিজ্ঞানের থেকেও অবাক করা! যে পথের শুরু হয়েছিল আইনস্টাইনের একটা জিজ্ঞাসা থেকে।
পুনশ্চ: সেই ‘প্রকৃতি-স্বরূপা’ ছাত্রী পরে বেলা স্যারের কাছে ক্ষমা চেয়েছিল। বেলা স্যারও আর কোনদিন কোন ছাত্রীকে মাদার নেচারের সাথে তুলনা করেননি।
~ এলেবেলের দলবল
► লেখা ভাল লাগলে অবশ্যই লাইক করুন, কমেন্ট করুন, আর সকলের সাথে শেয়ার করে সকলকে পড়ার সুযোগ করে দিন।
► এলেবেলেকে ফলো করুন।