~ কলমে এলেবেলে চিরশ্রী ~
ডিজিটাল ইলেকট্রনিক্সের ক্লাস চলছে। বোর্ডের উপর খসখস করে সার্কিট ডায়াগ্রাম এঁকে চলেছেন প্রফেসর বেদান্ত লাহা ওরফে বেলা স্যার। চোখটা বন্ধ হয়ে আসছে কাজুর, জোর করে তাকিয়ে খাতায় ছবিটা টুকছে সে। হঠাৎ একটা গোল পাকানো কাগজের ডেলা কাজুর পিঠে এসে লাগলো। ঝুঁকে মাটি থেকে তোলার আগেই খপ্ করে কাগজটা বাগিয়ে নিলেন বেলা স্যার। কিন্তু কি সব লেখা! “”নিপআ কি য়তানহীদ্রানি নছেগভু? গযোগাযো নরুক ২৪৪১১২৯””। কোনো মতে হাসি চেপে ফেললো কাজু। আলমটা কোন দিন বকুনি খাওয়াবে। তবে স্যার নিশ্চয়ই ধরতে পারেন নি আমাদের টোলউ ভাষা! কিন্তু ক্লাসের মধ্যিখানে কাগজ ছোঁড়াছুঁড়ি আর হিজিবিজি লেখার একটা জবাবদিহি উনি চাইতেই পারেন। মনে তখন অজুহাত সিন্থেসিস চলছে কাজু-আলমের।
“”নিপআ কি য়তানহীদ্রানি নছেগভু? গযোগাযো নরুক ২৪৪১১২৯””
“”তা বাছারা! একটু ভুল হয়ে গেল যে! শুধু নিদ্রাহীনতা নয়, অকালপক্কতারও চিকিৎসা হয় এই ঠিকানায়। আর বাবারা, নাম্বারটাও তো ভুল লিখেছিস দেখি! ওটা ২৪৪১১৩৯ হবে। গানটা অন্তত মন দিয়ে শোন! এত খারাপ সংকেতলিপি বানালে আমার মত বেলা স্যারও হেলায় তা হ্যাক করে ফেলবে! কি ভেবেছিলি! শব্দগুলো উল্টে দিলেই পার পেয়ে যাবি?”” বেলা স্যারের হেঁয়ালি কণ্ঠ তখন ক্লাসঘরে গমগম করছে।
তার পরের অভিজ্ঞতা না বলাই ভালো। তবে কাজু-আলমকে আমরা দোষ দিই না। সুরক্ষিত উপায়ে তথ্য আদান-প্রদান সেকালের রাজারাজরার আমল থেকে চলে আসছে। যুদ্ধ বা দেশের সুরক্ষা, ষড়যন্ত্র কিংবা ব্যক্তিগত ভাব বিনিময়, পৃথিবীর ইতিহাসে তথ্যের গুপ্তবেশ-এর (ডাটা এনক্রিপশন) ধারণা বেশ পুরনো। পুরো জিনিসটা অনেকটা একটা তথ্যে ভরা তালাবন্ধ সিন্দুকের মতন, যার চাবির খোঁজ শুধু দু’জনের জানার কথা। এক, যে পাঠাচ্ছে বা প্রেরক এবং দুই, যে গ্রহণ করছে, অর্থাৎ গ্রাহক। এখানে যেমন প্রেরক আলম নিজের বক্তব্যগুলো লিখলো, কিন্তু উল্টো করে। “”আপনি কি নিদ্রাহীনতায় ভুগছেন? যোগাযোগ করুন”” হল “”নিপআ কি য়তানহীদ্রানি নছেগভু? গযোগাযো নরুক””। গুপ্তবেশের পুরিয়া খুলে এই তথ্যটি উন্মোচন (ডি-কোড) করার চাবি আছে কাজুর কাছে। তাই আমাদের ক্লাসঘরের গ্রাহক সে। কিন্তু এবার যদি সিন্দুকের তালা অন্য কেউ খুলে ফেলতে পারে? আমাদের গল্পের সেই তালা ভাঙা হ্যাকার হলেন বেলা স্যার। সেকাল থেকে একাল অব্দি সুরক্ষিত তথ্য চালাচালির উদ্দেশ্যই হল এরকম বেলা স্যারদের হাত থেকে জরুরী তথ্যকে সুরক্ষিত রাখা।
সেকাল থেকে একাল অব্দি সুরক্ষিত তথ্য চালাচালির উদ্দেশ্যই হল এরকম বেলা স্যারদের হাত থেকে জরুরী তথ্যকে সুরক্ষিত রাখা।
আমরা এখন অনলাইন কেনাকাটা থেকে ব্যাঙ্কিং, যে কোনো রকম ব্যক্তিগত এবং রাষ্ট্রীয় তথ্য সুরক্ষিত রাখতে আস্থা রাখি কিছু গোপন কোড বা পাসওয়ার্ডের ওপর। আমাদের তথ্য ভরা সিন্দুকের তালাটিকে পাসওয়ার্ড, ওটিপি ও পিন এর খোঁচা ছাড়া খোলার উপায় নেই। কিন্তু এই তালার চাবি কি গ্রাহক ও প্রেরক ছাড়া অন্য কোনো তৃতীয় ব্যক্তির পক্ষে জাল করা সম্ভব? তা জানতে হলে তথ্যের ছদ্মবেশ বা এনক্রিপশনের ভাষা সম্পর্কে একটু জেনে নিতে হবে আগে।
প্রথমে আমরা এমন এক ছদ্মবেশের কথা আলোচনা করবো, বেলা স্যারেদের পক্ষে যাকে ভাঙা তাত্ত্বিক ভাবে খুব একটা জটিল না হলেও কার্যক্ষেত্রে তা অসম্ভবেরই সামিল। এই ছদ্মবেশের ধারক হল কিছু মৌলিক সংখ্যা। আমরা যে ক্লাসিকাল কম্পিউটার ব্যবহার করে থাকি, তার কাছে একটা সময় সাপেক্ষ কাজ হল কোনো সংখ্যার মৌলিক গুণনীয়ক বের করা, বা ইনটিজার ফ্যাক্টরাইজেশন। কিন্তু কেন?
আমরা জানি, একটা যৌগিক সংখ্যাকে সবসময় দুই বা ততোধিক মৌলিক সংখ্যার গুণফল হিসেবে প্রকাশ করা সম্ভব। অন্যদিকে, একটা সংখ্যা মৌলিক কিনা বোঝার জন্য আমাদের কি করণীয়? তার থেকে ছোট মৌলিক সংখ্যাগুলো দিয়ে সংখ্যাটিকে ভাগ করে করে দেখতে হবে সে বিভাজ্য কিনা। ধরা যাক, আমি আমার কম্পিউটারকে জিজ্ঞেস করলাম “”বলতো হে! ১১ মৌলিক না যৌগিক সংখ্যা?”” কি করবে সে?
কম্পিউটার প্রথমে ২ দিয়ে তাকে ভাগ করে দেখবে যে তা বিভাজ্য কিনা, না হলে ৩ দিয়ে, তাও না হলে ৫ দিয়ে। এভাবে যদি দেখা যায় ১১ সংখ্যাটি আগের কোনো মৌলিক সংখ্যা দ্বারা বিভাজিত হচ্ছে না, তাহলে ১১ কে মৌলিক হিসেবে চিহ্নিত করা যাবে। কিন্তু সংখ্যাটা যদি ২২৭ হয়? তাহলে কম্পিউটারকে আরেকটু বেশি খাটতে হবে, কারণ ২২৭ কে মৌলিক প্রমাণ করার জন্য কম্পিউটারকে ২ থেকে ১১৩ অব্দি প্রায় খান তিরিশেক মৌলিক সংখ্যা দিয়ে তাকে ভাগ করে দেখতে হবে। কম্পিউটারের খাটনি বা প্রযুক্তির ভাষায়, গণনার সময় (কম্পিউটিং টাইম) উত্তরোত্তর বৃদ্ধি পাবে সংখ্যাটার অঙ্ক যত বড় হবে। যেমন, ২০০৯ সালে একটি ২৩২ অঙ্কের (ডিজিট) অর্ধ-মৌলিক (সেমি-প্রাইম) সংখ্যার মৌলিক গুণনীয়ক নির্ণীত হয়। সংখ্যাটিকে মাত্র দু’টি মৌলিক সংখ্যার গুণফল হিসেবে প্রকাশ করা সম্ভব, তাই এটি অর্ধ-মৌলিক। এই কাজটা করতে একটা সাধারণ (এক কোর বিশিষ্ট ২.২ GHz AMD Opteron) কম্পিউটারের প্রায় ২০০০ বছরের সমান প্রসেসর টাইম লাগার কথা। আবার, ২০১৯ সালে খুঁজে পাওয়া ২৪০ অঙ্কের একটি অর্ধ-মৌলিক সংখ্যাকে দু’টি মৌলিক সংখ্যার গুণফল হিসেবে প্রকাশ করতে একটি (২.১ GHz Intel Xeon Gold ৬১৩০ CPU) সাধারণ কম্পিউটারের আনুমানিক ৯০০ কোটি বছর লাগবে। ক্লাসিকাল কম্পিউটারের এই ইনটিজার ফ্যাক্টরাইজেশনের দূর্বলতাই হতে পারে তথ্য সুরক্ষার ছদ্মবেশ বা ডাটা এনক্রিপশনের অস্ত্র। কীভাবে? দেখা যাক!
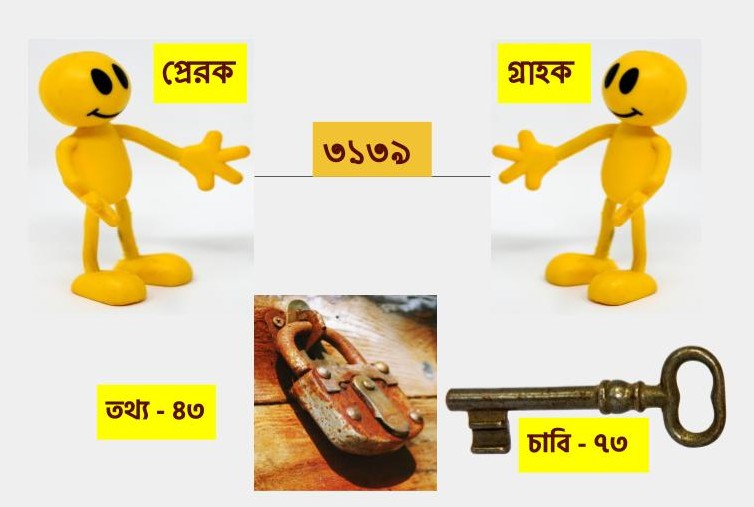
ধরা যাক আমার হাতে একটা কাগজ আছে। সেটাকে কয়েক টুকরোতে ছিঁড়ে ফেলা যত সহজ, ছেঁড়া টুকরোগুলোকে খাপে খাপ বসিয়ে জুড়ে ফেলা অসম্ভব না হলেও সময় সাপেক্ষ। একই ভাবে, ৪৩ এবং ৭৩, এই দু’টি মৌলিক সংখ্যাকে গুণ করে ৩১৩৯ বের করে ফেলা যতটা সহজ, উল্টোটা অর্থাৎ ৩১৩৯-এর মৌলিক গুণনীয়ক বের করা ততটা সহজসাধ্য কাজ নয়। সেটা করতে হলে কম্পিউটারকে ২..৩..৫..৭..১১.. মৌলিক সংখ্যাগুলির সাহায্যে প্রতিটা ধাপে ৩১৩৯-এর বিভাজ্যতা খুঁজতে হবে। এই কাজটা ততক্ষণ চালিয়ে যেতে হবে, যতক্ষণ না ৪৩ সংখ্যাটা আসছে। এবার ধরা যাক ব্যাঙ্কের কাছে থাকা আমার গোপনীয় টাকা পয়সার হিসেবকে একটি মৌলিক সংখ্যার ছদ্মবেশ দেওয়া হল। সংখ্যাটা ধরলাম ৪৩। যে তথ্যটি ব্যাঙ্ক আমাকে পাঠাবে, সেটি ৩১৩৯ সংখ্যাটির ভেক ধরে হাজির হল। আমার কাছে থাকা পাসওয়ার্ডটি হচ্ছে ৭৩। হিসেব মত, একমাত্র গ্রাহক অর্থাৎ আমিই পারি ৩১৩৯ কে ৭৩ দিয়ে ভাগ করে ৪৩ নম্বরের পেছনে লুকিয়ে থাকা ছদ্ম তথ্যটা হাতে পেতে (ছবি: ওপরে)। এবার আসি হ্যাকারের কথায়। সে দেখতে পাবে শুধু ৩১৩৯ সংখ্যা-রূপী তথ্যটা। সে গুণনীয়কগুলো, অর্থাৎ তথ্য ৪৩ এবং পাসওয়ার্ড ৭৩ কোনোটাই জানে না। ইনটিজার ফ্যাক্টরাইজেশনের কাজটা তাকে নিজে করতে হবে (ছবি: নিচে)। এইবারে, সংখ্যাটা চার অঙ্কের না হয়ে যদি ১০০ বা ২০০ অঙ্কের হয়, তাকে ভাঙতে হ্যাকারের কাছে থাকা সুপার কম্পিউটারের হয়তো বছর খানেক সময় লেগে যাবে। যত বড় সংখ্যা দিয়ে ব্যাঙ্ক তথ্যটাকে লুকাবে, তাকে ভাঙার জন্য ততো জাঁদরেল সুপার কম্পিউটারের মালিক হতে হবে আমাদের হ্যাকারকে। সেই কারণেই এই ধরনের হ্যাকিং তাত্ত্বিক ভাবে অসাধ্য না হলেও কার্যত ভীষণই দুরূহ।

এবার চলে আাসি ২০১৯ সালে। যারা প্রযুক্তি দুনিয়ার খোঁজ রাখেন, “”কোয়ান্টাম সুপ্রিমেসি”” বলে একটা কথা হয়তো তারা শুনে থাকবেন। ২০১৯ সালের অক্টোবর মাসে নেচার পত্রিকায় প্রকাশিত একটি গবেষণাপত্রের তথ্য অনুযায়ী, গুগল কোম্পানি কোয়ান্টাম প্রযুক্তির সাহায্য নিয়ে এমন কিছু জটিল গাণিতিক সমস্যার সমাধান করে ফেলতে সক্ষম মাত্র ২০০ সেকেন্ডে, যা গণনা করতে একটা ক্লাসিকাল সুপার কম্পিউটারের লাগার কথা আনুমানিক ১০,০০০ বছর। আর এখানেই চলে আসে সবথেকে বড় প্রশ্নটা। ক্লাসিকাল প্রযুক্তির যে দূর্বলতাকে কাজে লাগিয়ে তৈরি হয়েছে তথ্য সুরক্ষিত রাখার কৌশল, কোয়ান্টাম প্রযুক্তির হাতে ক্ষমতা আছে হেলায় সেই দূর্বলতাকে কাটিয়ে ফেলার। তাহলে কোয়ান্টাম জমানায় আমাদের গোপন কথা কি আদৌ গোপনে রাখা সম্ভব?
এরকম কোনো ছদ্মবেশ ব্যবহার করা কি সম্ভব, যা ভাঙা শুধু দুরূহ নয়, অসম্ভব! আর এখান থেকেই শুরু হয় কোয়ান্টাম এনক্রিপশনের ধারণা। যে কোয়ান্টাম প্রযুক্তির হাতে তালা ভাঙার অসীম ক্ষমতা আছে, সেই প্রযুক্তির সাহায্য নিয়েই তৈরি করা সম্ভব এমন একটি তালা, যা ভাঙতে হলে কোয়ান্টাম গতিবিদ্যার সূত্রগুলোকেই ভেঙে ফেলতে হবে! ভাঙতে হবে প্রকৃতির নিয়ম!
একটি তালা, যা ভাঙতে হলে কোয়ান্টাম গতিবিদ্যার সূত্রগুলোকেই ভেঙে ফেলতে হবে! ভাঙতে হবে প্রকৃতির নিয়ম!
কোয়ান্টাম যে আণুবীক্ষণিক দুনিয়ার কথা বলে, সেখানে কোনো বস্তুর ভর এবং ভরবেগ একসঙ্গে নির্ভুল উপায়ে মাপা সম্ভব নয়। আণুবীক্ষণিক বস্তুর এই গোলমেলে স্বভাবকে প্রথম চিনেছিলেন পদার্থবিদ হেইজেনবার্গ (এ বিষয়ে বিশদে জানতে হলে কোয়ান্টামের কড়চার ‘পর্ব-২’ এবং ‘পর্ব-৩’ পড়ে ফেলতে হবে)। তাঁর শেখানো অনিশ্চয়তা নীতির ওপরেই দাঁড়িয়ে এমন এক তথ্য গোপনের ছদ্মবেশ, যাকে ভাঙতে হলে হেইজেনবার্গের অনিশ্চয়তা নীতিকেই ভাঙার চেষ্টা করতে হবে, যা আণুবীক্ষণিক বস্তু জগতের স্বকীয় ধর্ম কখনোই হতে দেবে না। তাই হ্যাকার যতই চেষ্টা করুক না কেন, গোপন কথাটি রয়ে যাবে গোপনে।
এখন প্রশ্নটা হচ্ছে, এই কোয়ান্টাম প্রযুক্তি কীভাবে কাজ করে?
সেটা জানতে আমাদের অপেক্ষা করতে হবে পরবর্তী পর্বের জন্য।
এলেবেলের দলবল
► লেখা ভাল লাগলে অবশ্যই লাইক করুন, কমেন্ট করুন, আর সকলের সাথে শেয়ার করে সকলকে পড়ার সুযোগ করে দিন।
► এলেবেলেকে ফলো করুন।